| Accueil | Mathématiques | Images |
L'objet de cette page est de présenter une étude personnelle du problème de Syracuse. Après une introduction du problème dans sa forme classique, différents points de vue - heuristique, combinatoire, géométrique, musical - seront esquissés. Une étude basée sur une extension réelle et complexe sera développée, puis généralisée. Des diagrammes de bifurcation seront présentés. Enfin nous décrirons la dynamique asymptotique ainsi obtenue.
Séquences de Collatz
Une séquence de Collatz s'obtient à partir d'un entier n de départ auquel on applique de manière itérative la fonction
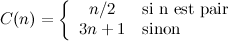
Par exemple, si l'on part de la valeur n = 7, on obtiendra la suite :
7 ; 22 ; 11 ; 34 ; 17 ; 52 ; 26 ; 13 ; 40 ; 20 ; 10 ; 5 ; 16 ; 8 ; 4 ; 2 ; 1 …
Cette suite boucle indéfiniment sur le cycle {1 ; 4 ; 2}. Et cela semble se produire quelque soit la valeur choisie initialement, bien que le nombre d'étapes soit parfois étonnement élevé avant d'y parvenir. Par exemple, la valeur 27 génère une suite de 111 termes différents.
La conjecture de Syracuse est que toute itération de cette fonction à partir d’un entier naturel non-nul aboutit invariablement à la valeur 1. Elle a été formulée par Lothar Collatz et a commencé à circuler avant d'être diffusée à l'université de Syracuse.Entre 2004 et 2009, Tomás Oliveira e Silva a vérifié par ordinateur que la conjecture est vraie pour tout entier n < 5*1018. Plus récemment, David Barina a poursuivi la vérification jusqu'à 268 ≈ 2,95*1020 avec un nouvel algorithme, de septembre 2019 à mai 2020. [Bar20]
Néanmoins, ce problème n'a pas encore été résolu à ce jour. Les nombreuses recherches [Lag-I] [Lag-II] qu'il a suscitées ont donné lieu à plusieurs avancées significatives. Par exemple, les résultats de Shalom Eliahou [Eli93] [Eli11] permettent d'affirmer que s'il existe un autre cycle que {1 ; 4 ; 2}, alors sa longueur est supérieure à 1,8*1011 en tenant compte du dernier seuil de vérification atteint par Barina en 2020.
Un autre résultat notable, obtenu par Ilia Krasikov et Jeffrey Lagarias [Kra03], est que le nombre d'entiers inférieurs à X et dont l'orbite aboutit à 1 est au moins égal à X0,84 pour tout entier X suffisamment grand.
Par ailleurs, la conjecture de Syracuse pourrait aussi être vraie tout en étant impossible à démontrer, ce qui en ferait un problème indécidable.
On pourra consulter les divers ouvrages bibliographiques réalisés par Marc Chamberland [Cha03], Jeffrey Lagarias [Lag-I] [Lag-II] [Lag11], Günter Wirsching [Wir98] ou encore Luc-Olivier Pochon et Alain Favre [Poc17] pour une synthèse détaillée des connaissances autour du problème de Syracuse et ses nombreux avatars.
Argumentation heuristique
Essayons de comprendre pourquoi la suite de Collatz a tendance à décroître, quel que soit le point initial.Un entier n choisi au hasard a une chance sur deux d'être pair. Dans ce cas, il sera divisé par 2, sinon il sera multiplié par 3 et augmenté de 1. Le terme suivant a-t-il lui aussi une chance sur deux d'être pair ? La réponse est non : dans le 2ème cas, la valeur 3n+1 est toujours paire.
Pour cette raison, il est souvent convenu de remplacer la fonction C par la fonction :
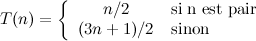
Par exemple, la valeur n=7 produira cette fois la suite accélérée :
7 ; 11 ; 17 ; 26 ; 13 ; 20 ; 10 ; 5 ; 8 ; 4 ; 2 ; 1 .
On aboutit alors au cycle {1 ; 2}.
A présent, il semble que les images successives d'un entier arbitrairement grand par la fonction T ont autant de chance d'être paires que d'être impaires. Cela revient à dire que le terme courant est multiplié par 1/2 ou par 3/2 avec la même probabilité 1/2 à chaque itération. En moyenne géométrique, le facteur multiplicatif est égal à
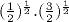 =
= 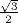 = 0,866... [Bar98].
= 0,866... [Bar98].On peut donc s'attendre à voir décroître les suites de Collatz. Evidemment, cet argument est d'ordre spéculatif et il ne s'agit nullement d'une preuve. Toutefois des calculs numériques suggèrent que l'on capture de cette manière l'essentiel de la dynamique asymptotique. En échelle logarithmique, les trajectoires s'apparentent à une marche aléatoire à une dimension. Comme les pas descendants sont plus grands, on dira que la marche aléatoire est anisotrope.
Par un raisonnement heuristique similaire, Richard Crandall [Cra78] a estimé que le rapport entre deux termes impairs est en moyenne égal à 3/4.
Note : on s'amusera à vérifier qu'un joueur qui miserait systématiquement la moitié de ce qu'il possède à quitte-ou-double en jouant à pile-ou-face a de fortes chances de s'appauvrir (à moins qu'il ne fasse sauter la banque, mais c'est peu probable...). Cela ressemble à une martingale inversée ...
De faît, Riho Terras [Ter76] [Ter79] a prouvé que l'ensemble des entiers dont l'orbite ne descend jamais plus bas que l'entier de départ a une densité nulle dans l'ensemble des entiers naturels.
Terrence Tao [Tao22] a réalisé en 2019 une percée très convaincante. Il démontre que pour toute fonction F agissant sur les entiers positifs et tendant vers l'infini, la proportion d'entiers n dont l'orbite descend en-dessous de F(n) tend asymptotiquement vers 1. La force de ce résultat est qu'il reste vrai même si l'on choisit une fonction F à croissance très lente, comme le logarithme. Mais il ne dit rien sur les orbites qui arrivent jusqu'à 1, ni même sur les orbites bornées. C'est donc insuffisant pour conclure.
Représentation géométrique
Une réprésentation possible des itérations de la fonction T(n) est de placer les entiers sur une spirale, de telle sorte que les entiers qui se déduisent les uns des autres par une multiplication ou une division par une puissance de 2 soient tous alignés. On relie ensuite chaque entier n à son image T(n) par un segment de droite, rouge si l'entier de départ est pair, et vert s'il est impair.Plus précisement, chaque entier n>0 aura pour coordonnées polaires :
rn = n
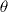 n
= 2
n
= 2 ln(n) / ln(2)
ln(n) / ln(2)Ainsi, l'ensemble des entiers se positionnera sur la spirale logarithmique d'équation :
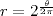
Ensuite, afin d'éviter que les segments ne se croisent dans le plan, nous ferons appel à la 3ème dimension et affecterons une hauteur à chaque entier n :
zn = n
Nous obtenons alors une spirale ascendante, qui s'enroule autour d'un cône invisible, pointé vers le bas.
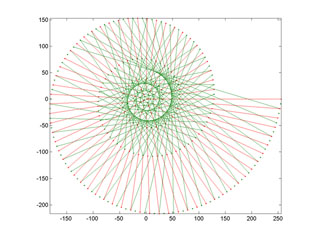 Liens entre les entiers
de 1 à 256, vue de haut
|
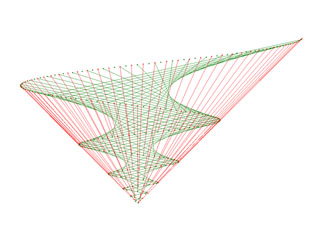 Liens entre les entiers
de 1 à 256, vue de profil
|

Analogie musicale
Il existe
une forte analogie entre le problème de Syracuse et la théorie
musicale. Considérons en effet les entiers comme des notes de musique
caractérisées par leur fréquence. Ainsi, la division par 2 d'un entier
pair revient à descendre d'une octave. Tandis qu'une multiplication par
3/2 d'un entier impair s'apparente à une quinte. La gamme
pythagoricienne est précisément basée sur les deux accords jugés les
plus harmonieux que sont l'octave et la quinte. Une gamme de 12 notes a
été définie et largement utilisée car une série de 12 quintes aboutit à
un son très proche du son de départ remonté de 7 octaves.
C'est le cycle des quintes. Mathématiquement, nous pouvons
effectivement vérifier que (3/2)^12 =
129.746... ≈
2^7 = 128, ou encore que ln 3/ln 2 ≈ 19/12.
Il se trouve que la recherche de cycles dans le problème de Syracuse est étroitement liée aux approximations rationnelles de ln 3/ln 2 [Cra78] [Eli93] [Roz90].
Encore
aujourd'hui, nous utilisons la gamme tempérée obtenue en divisant
l'octave en 12 demi-tons chromatiques égaux avec un rapport de
fréquence de 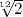 .
.
Automates cellulaires
Une autre visualisation possible du problème de Syracuse consiste à représenter les entiers sur une grille composée de petites cellules [Ger04]. Pour ce faire, on utilisera l'écriture en base 2. Ainsi, chaque cellule peut se trouver dans l'un des trois états possibles : état "vide", état "0" ou état "1". Comme l'étape de division par 2 dans une séquence ne change pas la représentation, à un décalage près des cellules, on choisit de représenter seulement les termes impairs de la séquence, disposés ligne par ligne. Cette représentation s'apparente à un automate cellulaire linéaire dont les règles d'évolution sont un peu particulières. En effet, l'état d'une cellule dépend non seulement des cellules voisines qui la précédent, mais parfois aussi de cellules plus éloignées lorsqu'une retenue se propage. Toutefois, on tentera de réduire la distance entre les cellules ayant les plus fortes interactions. Pour cette raison, on n'effectue pas le décalage associé aux divisions par 2. Il en résulte une dérive du motif cellulaire vers la gauche, jusqu'à atteindre une puissance de 2, comme dans l'exemple simple ci-dessous.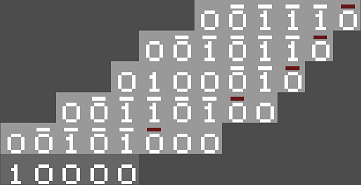 |
| Orbite impaire de l'entier 7 7 → 11→ 17 → 13 → 5 → 1 |
Les traits horizontaux signalent la présence d'une retenue lors du calcul d'une itération. Cette image a été réalisée avec le logiciel SimCQCA de Tristan Stérin, qui a découvert la remarquable propriété suivante : cet automate calcule les suites de Syracuse en base 2 (horizontalement), mais aussi en base 3 (verticalement) et en base 6 (en diagonal), de manière simultanée ! Pour le voir, il suffit d'augmenter le nombre d'états en tenant compte des retenues. [Sté20]
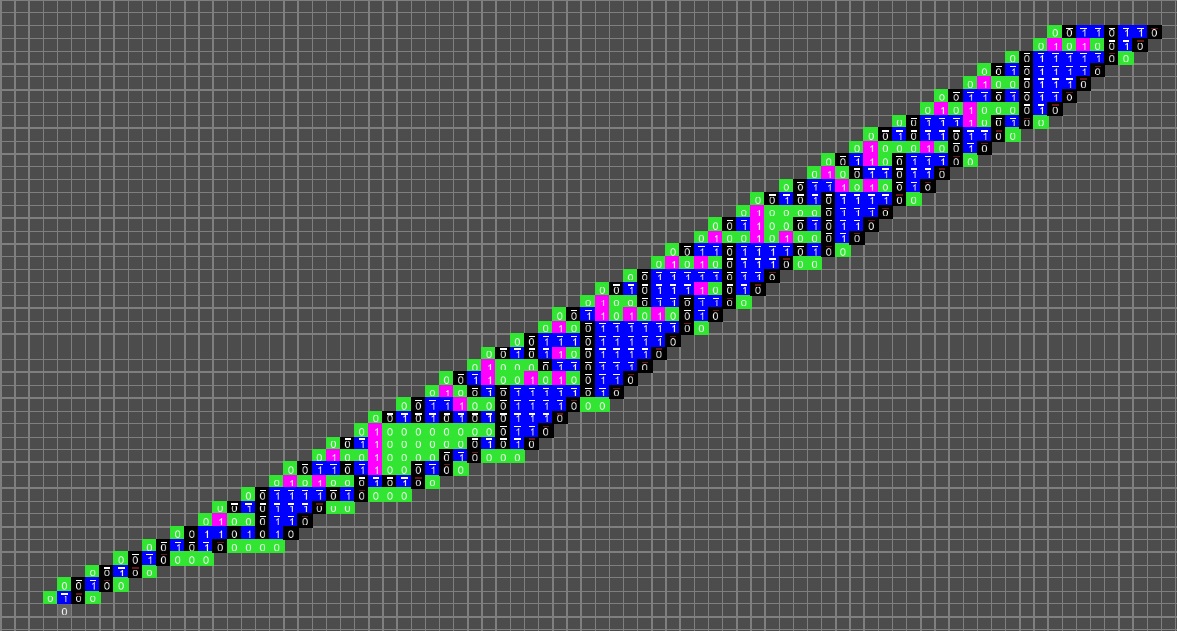 |
| Orbite impaire de l'entier 27 avec SimCQCA |
Marches aléatoires
Le concept de marche alétoire a été exploité pour construire des modèles probabilistes (ou stochastiques) du problème de Syracuse. L'objectif est de mieux comprendre la dynamique des itérations, caractérisée par deux indicateurs :- le temps
de vol, noté
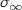 (n),
(n),
- l'altitude
maximale, notée t(n).
A titre d'exemple, on a pour l'entier n=27 les valeurs étonnament élevées
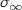 (27) = 70 et
t(27) = 4616.
(27) = 70 et
t(27) = 4616.Grâce à la théorie probabiliste des grandes déviations, le modèle de marche aléatoire [Lag11] a permis d'estimer, asymptotiquement, une borne supérieure pour chacun des indicateurs précédents :
Entropie binaire
Un moyen
simple de décrire la dynamique d'une séquence qui part de l'entier n consiste
à noter les parités successives des termes qui la composent sous la
forme d'une suite de '0' et de '1'. Une telle suite se nomme vecteur
parité associé à n.Par exemple, l'entier n=7 conduit au vecteur parité (1, 1, 1, 0, 1, 0, 0, 1, 0, 0) sur 10 itérations de T.
Un résultat de Riho Terras [Ter76] affirme que tout vecteur parité de longueur j est associé à exactement un entier compris entre 1 et 2j. On en déduit que le nombre d'entiers entre 1 et 2j qui génèrent q termes impairs sur j itérations s'exprime au moyen du coefficient binomial :
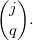
On peut alors s'intéresser à la répartition de ces entiers entre 1 et 2j, et l'on constate que cette répartition semble souvent aléatoire lorsque j/2 < q < j. Cela nous amène à formuler une hypothèse [Roz17] sur la borne inférieure de cette famille d'entiers grâce à la fonction d'entropie binaire
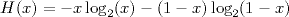
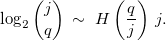
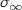 (n), et de
l'altitude maximale t(n) d'un entier n. De plus, on montre que la
constante γ vérifie
(n), et de
l'altitude maximale t(n) d'un entier n. De plus, on montre que la
constante γ vérifie 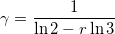
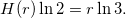
Extensions
L'idée est de prolonger la fonction T par une fonction continue, définie sur l'ensemble des nombres réels ou complexes. Cela permettra d'appliquer des outils mathématiques issus de la théorie des systèmes dynamiques, et accessoirement, de générer d'étonnantes images fractales.
Extension
réelle
Il a été proposé [Aou90] [Cha96] de prolonger la fonction T(n) discrète par la fonction continue suivante, définie sur l’ensemble des nombres réels :
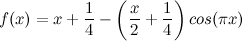
Pour chaque entier n, on a f(n) = T(n).
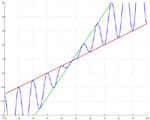 |
La courbe y = f(x) est parfaitement délimitée par les droites y = x/2 et y = (3x+1)/2.
Le nombre de points fixes est infini (intersections avec la droite y=x), et seulement deux sont attractifs : 0 et –1,277733766…. Le point fixe –1 est répulsif, ainsi que les autres points fixes non-entiers.
Lorsque l’on étudie les itérations de la fonction f(x) dans l’ensemble des réels, on trouve un certain nombre de cycles attractifs dont un cycle entier et cinq non-entiers :
- {1 ; 2}
- {1,192531… ; 2,138656…}
- {-4,998739… ; -6,998091… ; -9,997078…}
- {-5,046002… ; -7,045307… ; -10,034865…}
- {-16,999991… ; -24,999987… ; -36,999981… ; -54,999971… ; -81,999957…; -40,999979… ; -60,999968… ; -90,999952… ; -135,999928… ; -67,999965… ; -33,999983…}
- {-17,002728… ; -25,003789… ; -37,004815… ; -55,005134… ; -82,004156…; -41,005552… ; -61,005247… ; -91,003760… ; -136,002482… ; -68,003302… ; -34,003467…}
- {-5 ; -7 ; -10}
- {-17 ; -25 ; -37 ; -55 ; -82 ; -41 ; -61 ; -91 ; -136 ; -68 ; -34}
La plupart des nombres réels convergent soit vers l’un des deux points fixes attractifs, soit vers l'un des quatre cycles attractifs précédents. Mais d'autres nombres ne se comportent pas ainsi, en particulier les points fixes répulsifs.
Une question cruciale est de déterminer si certains nombres réels conduisent à une suite non-bornée. En effet, l'inexistence de telles suites aurait des implications très importantes en faveur de la conjecture de Syracuse. Cependant, Marc Chamberland [Cha96] a démontré que de telles suites de nombres réels existent, certaines ayant même une croissance monotone, et il est conjecturé que ces suites de nombres réels forment un ensemble non-dénombrable de "mesure nulle" dans l'ensemble des réels positifs.
En
faît, une analyse
asymptotique sur un
grand nombre d'itérations de la fonction f(x) au
voisinage de l'infini suggère une décroissance moyenne
d'un facteur 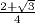 = 0,933... à chaque itération,
dans l'ensemble des réels. Mais ceci ne s'applique pas à tous les
réels, et en particulier aux entiers qui ont un comportement différent
de celui de la plupart des réels.
= 0,933... à chaque itération,
dans l'ensemble des réels. Mais ceci ne s'applique pas à tous les
réels, et en particulier aux entiers qui ont un comportement différent
de celui de la plupart des réels.
Or,
les
entiers ont semble-t-il une décroissance moyenne plus rapide, puisque
le rapport
moyen entre deux itérés successifs de la fonction T(n) est 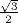 =0,866... (moyenne géométrique de
=0,866... (moyenne géométrique de 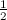 et
et 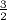 ).
).
Il est
curieux que la valeur 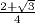 soit
précisément égale à la moyenne arithmétique de
soit
précisément égale à la moyenne arithmétique de 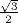 et 1.
et 1.
Le grand intérêt de cette extension est que la dynamique de la fonction f sur les réels est intrinsèquement liée à celle de la fonction T sur les entiers. Avec Nik Lygeros [Lyg14] nous avons ainsi montré que le problème de Syracuse se ramène entièrement à l'étude de la dynamique des points critiques de f proches des entiers naturels impairs.
Extension complexe
On peut
aisément étendre le domaine
d’étude à
tous les nombres complexes [Aou90],
puisque la fonction f est
définie mathématiquement sur  .
.
A
première vue, une
telle généralisation ne simplifie pas
l’étude,
bien au contraire. Toutefois elle permet de visualiser les bassins
d’attraction dans un espace à deux dimensions, et
donc
d’obtenir des images qui pourront éventuellement
guider
notre intuition. L’apparition de formes fractales n’est guère une
surprise puisque le principe de
construction est analogue aux ensembles
de Julia. Nous appellerons "ensemble
de Collatz" l'ensemble des
orbites bornées de f
dans  .
.
On notera la proportion importante de nombres complexes, en-dehors de l'axe des réels, conduisant à une orbite non-bornée.
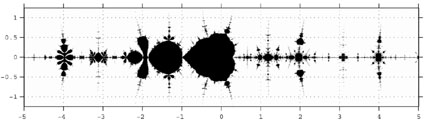 Ensemble
de Collatz
|
Visuellement, on remarque une certaine ressemblance avec l'ensemble de Mandelbrot. Mais d'un point de vue topologique, il y a de nombreuses différences : tandis que ce dernier est borné, fermé et connexe, l'ensemble de Collatz ne possède aucune de ces propriétés. Il est en faît déconnecté en une infinité de composantes très proches les unes des autres, comme des perles sur un collier dont le fil est invisible.
L'exploration de l'ensemble de Collatz au voisinage des entiers relatifs mérite le détour. Des images sont visibles ici.
Paramétrisation
Le problème de Syracuse, appelé aussi « problème 3x+1 », possède diverses variantes. Par exemple en remplaçant la valeur 3 par un entier impair q > 3, on est conduit à l'étude des « problèmes qx+1 » introduits par Crandall [Cra78]. On peut ainsi définir la fonction entière suivante :
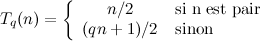
Lorsque q > 3, les itérations semblent globalement tendre vers l'infini, dans la plupart des cas.
En procédant comme précédemment, nous pouvons étendre la fonction Tq à l’ensemble des réels :
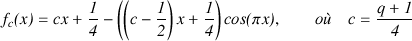
Il est aisé de vérifier que fc(n) = Tq(n) pour tout entier n.
Chaque courbe y = fc(x) est parfaitement délimitée par les droites y = x/2 et y = (2c - ½)x + ½.
Le problème de Syracuse correspond à la valeur c=1 sur l’ensemble des entiers positifs. L’intérêt de cette paramétrisation est de permettre une évolution continue du paramètre c dans l’ensemble des nombres réels, et d'étudier ainsi finement la transition entre les variantes convergentes sur les entiers (q=1 ou 3) et les variantes divergentes (q=5, 7, 9 ...).
Remarquons que les variantes du type « qx-1 » sont également obtenues en se plaçant du côté des nombres négatifs. En effet, si q est un entier impair et n un entier positif , on aura :
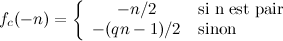
Diagrammes de bifurcation
Le comportement des itérations successives de fc pour un même point initial peut changer qualitativement suivant les valeurs du paramètre c : on observe souvent un dédoublement des points attractifs. Ainsi la convergence vers un point fixe cédera la place à un cycle de 2 points attractifs, puis 4, 8, 16 ... L'issue de ce processus en cascade est souvent l'irruption d'un régime chaotique. Ce phénomène, intrinsèquement présent dans nombre de systèmes dynamiques, a un caractère universel.Les diagrammes de bifurcation permettent de représenter sur une seule image les points d'accumulation obtenus par itération de la fonction fc sur une plage de valeurs du paramètre c, en abscisse. On observera ainsi des structures arborescentes avec de nombreuses ramifications et l'apparition de régimes chaotiques localisés. La visulalisation des densités de probabilité est possible avec l'utilisation de plusieurs niveaux de gris (échelle logarithmique).
Par exemple, lorsque c > 1/4, le comportement itératif de fc dans l'intervalle [0 ; 2,5] est modifié pour les valeurs de c suivantes :
|
apparition de la branche principale |
|
ramification de la branche principale en deux branches |
|
apparition d'une deuxième double-branche sur laquelle on trouve le cycle {1,192531…; 2,138656…} de la fonction f1 |
|
disparition de la double-branche issue de la branche principale sur laquelle on trouve le cycle {1; 2}de la fonction f1 |
|
début de la ramification en cascade de la deuxième double-branche |
|
début du régime chaotique |
|
régime chaotique non-borné |
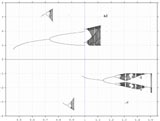 0,4
< c < 1,55
|

0,98
< c < 1,13
|
Notons que la valeur c=1 se trouve précisément à l'intérieur de l'étroite bande [0,991154... ; 1,000968...] dans laquelle coexistent deux cycles attracteurs de période 2.
Diagrammes d'attraction
A chaque diagramme de bifurcation, il est possible d'associer un diagramme d'attraction, sur lequel on visualise l'évolution continue des bassins d'attraction de la fonction fc dans l'ensemble des réels sur une plage de valeurs du paramètre c, en abscisse. Les images suivantes illustrent l’effet des ramifications de cycles attracteurs sur les bassins d’attraction, de plus en plus intriqués. Diagramme d'attraction de fc Diagramme d'attraction de fc 0,979 < c < 1,038 |
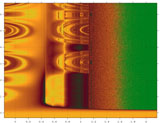 Diagramme d'attraction de fc -0,166 < c < 2,166 |
Sur le diagramme ci-dessous, on visualise la frontière des bassins d'attraction en noir, et les attracteurs en rouge :
|
Diagramme
de bifurcation et contours des bassins d'attraction 0,98 < c < 1,13 |
Analyse asymptotique
On s'intéressera dans cette partie au pouvoir attractif de l'infini, sur les réels non-entiers.Voici les questions qui vont être traitées, plus précisémment :
- comment prédire le comportement asymptotique moyen des itérés au voisinage de l'infini ?
- à quelle vitesse moyenne se produit, selon les cas, la croissance ou la décroissance des itérations au voisinage de l'infini ?
- pour quelles valeurs du paramètre c la famille de fonctions {fc} bascule-t-elle d'un comportement moyen décroissant à un comportement moyen divergent à l'infini ?
Pour connaître le comportement asymptotique moyen des itérés, il faudrait estimer la valeur moyenne du rapport fc(x)/x. En effet, si l'on dispose d'une telle valeur moyenne
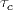 , alors
on pourra essayer de déterminer la croissance ou la décroissance sur un
grand nombre d'itérations, et sous certaines conditions.
, alors
on pourra essayer de déterminer la croissance ou la décroissance sur un
grand nombre d'itérations, et sous certaines conditions.Or la fonction fc(x)/x possède une asymptote sinusoïdale y =
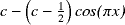 , de
période 2. :
, de
période 2. :
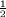 cos(
cos( x)
, en rouge
x)
, en rougeLa moyenne géométrique de la courbe asymptote, sur une période, a la valeur suivante :
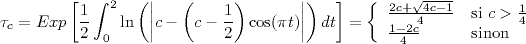
Pour c=1, on obtient la valeur moyenne
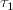 =
= 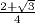 =
0,933012...
=
0,933012...On vérifie aisément que
 <
1 si et seulement
si
<
1 si et seulement
si 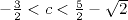 .
.Il semble ainsi que les seuils du basculement entre les comportements globalement décroissants puis croissants se produisent lorsque c = -
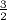 et c
=
et c
= 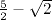 = 1,085786...
= 1,085786...Ceci nous amène à énoncer la conjecture suivante :
CONJECTURE
Les itérations de la fonction fc sont décroissantes en moyenne pour presque tout réel x au voisinage de
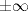 , si et
seulement si on a
:
, si et
seulement si on a
: 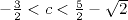
Une application numérique simple permet de vérifier pour différentes valeurs de c, et x aléatoirement choisi entre -10150 et 10150, que le taux moyen de croissance est souvent très proche de
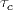 :
: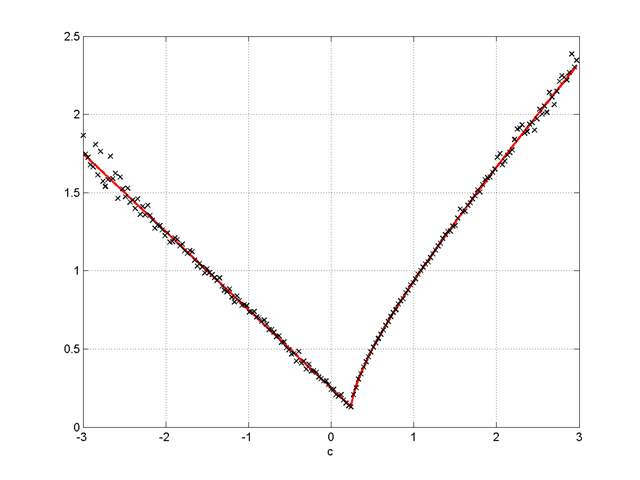 Comparaison du taux
moyen de croissance sur 1000 itérations
avec les valeurs asymptotiques 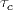 (en rouge)
(en rouge) |
Cependant tous les réels x au voisinage de
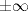 ne vont
pas se comporter ainsi. Par
exemple les nombreux points
fixes auront un taux de croissance toujours égal à 1, et les puissances
de 2 un taux égal à 1/2, pour toute valeur de c.
ne vont
pas se comporter ainsi. Par
exemple les nombreux points
fixes auront un taux de croissance toujours égal à 1, et les puissances
de 2 un taux égal à 1/2, pour toute valeur de c.On montre que si c>1/4, alors une condition suffisante pour que le taux moyen de croissance d'un réel x suffisamment grand soit proche de
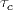 est que
la discrépance modulo 2 de ses
itérés soit faible : les valeurs modulo 2 de ses itérés successifs
doivent être réparties assez uniformément dans
l'intervalle [0 ; 2) [Lyg19].
est que
la discrépance modulo 2 de ses
itérés soit faible : les valeurs modulo 2 de ses itérés successifs
doivent être réparties assez uniformément dans
l'intervalle [0 ; 2) [Lyg19].Lorsque c ≤ 1/4, cette condition n'est pas suffisante car la fonction fc possède alors une infinité de zéros (voir graphe) au voisinage de
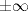 . Il faut analyser
plus finement la répartition des itérés et la proximité éventuelle des
zéros de la fonction fc.
. Il faut analyser
plus finement la répartition des itérés et la proximité éventuelle des
zéros de la fonction fc.Perspectives
J'espère avoir apporté un éclairage original et une meilleure compréhension du problème de Syracuse. Diverses interprétations laissent entrevoir des connexions déroutantes dans des domaines parfois éloignés. Ainsi, le prolongement de la fonction de Collatz aux nombres réels et complexes élargit l'espace de recherche et amène toute une panoplie de nouveaux outils. D'une part, il existe des liens étroits entre le problème de Syracuse et la dynamique de l'extension réelle proposée [Lyg14]. D'autre part, l'introduction d'un paramètre réel suggère que nous sommes proches de la frontière entre croissance et décroissance. Or c'est justement au voisinage d'une telle frontière que se multiplient les comportements chaotiques complexes inhérents à de nombreux systèmes dynamiques.Au lieu de ne considérer qu'un seul paramètre, nous pouvons aussi en introduire plusieurs, ce qui amène des degrés de liberté supplémentaires. Dans une étude récente [Lyg19], nous avons ainsi obtenu un diagramme de phase bidimensionnel afin de caractériser le comportement moyen des itérations réelles avec une dépendance à quatre paramètres.
La même méthode est applicable à d'autres extensions réelles et complexes issues de diverses publications. Par exemple, une extension continue et linéaire par morceaux semble à la fois simple et naturelle. La dynamique est alors toute autre car la forte pente au voisinage des entiers fait disparaître les bassins d'attraction.
Par ailleurs, nous pouvons étendre le problème à des espaces plus exotiques comme celui des entiers 2-adiques, qui ont une écriture en base 2 infinie vers la gauche. En un sens, la situation est plus simple car la fonction T admet une unique extension continue pour la topologie 2-adique. Elle génère une dynamique ergodique [Mat84], donc dépourvue de bassin d'attraction. Cette approche constitue un axe de recherche actif. A titre d'exemple, elle a récemment conduit à la découverte de structures autosimilaires, imparfaitement comprises bien que visualisables grâce à des plongements euclidiens [Roz19].
En dépit des progrès effectués par intermittence, la résolution du problème de Syracuse parait toujours hors de portée. Les mathématiques sous-jacentes sont-elles encore en gestation ? Ou existe-t-il une difficulté intrinsèque d'un autre ordre ?
Annexe
Autres extensions
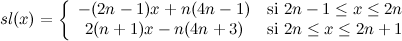
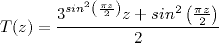
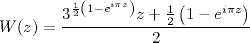
La fonction W(z), nommée "Winding", ne préserve pas les réels.
- Extension
de T sur
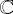 ,
continue, proposée
par S.
Letherman, D. Schleicher et R. Wood [Let99]
,
continue, proposée
par S.
Letherman, D. Schleicher et R. Wood [Let99]
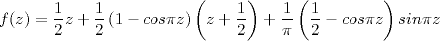
Les entiers sont des points critiques.
-
Extension de C sur
 , non-continue, proposée par J. L. Pe [Pe04]
, non-continue, proposée par J. L. Pe [Pe04]
-
Extension de C sur
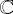 , continue, proposée par Gilles
Godefroy
, continue, proposée par Gilles
Godefroy
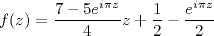
Cette extension ne préserve pas les réels.
-
Extension de T sur les réels positifs, continue, proposée par Rénald Simonetto [Sim17]
Elle peut être prolongée analytiquement
sur  \ (-1/3 ; 0), avec un point
singulier en -1/3.
\ (-1/3 ; 0), avec un point
singulier en -1/3.
Références
[Aou90] A. Aoufi & O. Rozier, Le problème de Syracuse dans C, Singularité N°5 (1990).
[Bar20]
D. Barina, Convergence
verification of the Collatz problem, J. Supercomputing (2020).
[Bar98]
E. Barone, Una argumentazione
euristica probabilistica sulla successione di Collatz, Ital. J.
Pure Appl. Math. 4 (1998).
[Cha96] M. Chamberland, A Continuous Extension of the 3x+1 Problem to the Real Line, Dyn. of Contin., Discrete and Impuls. Syst., 2 (1996).
[Cha03] M. Chamberland, An update on the 3x+1 problem (2003).
[Cra78] R. E. Crandall, On the 3x+1 problem, Math.
Comp. 32
(1978).
[Del98] J-P. Delahaye, La conjecture de Syracuse, Pour La Science N°247 (1998).
[Dum01] J. Dumont & C. Reiter, Visualizing generalized 3x+1 function dynamics, Computers & Graphics, Volume 25, Issue 5 (2001).
[Dum03] J. Dumont & C. Reiter, Real dynamics of a 3-power extension of the 3x+1 function, Dynamics of Continuous, Discrete and Impulsive Systems, Volume 10 (2003).
[Eli93]
S. Eliahou, The 3x+1 problem: new lower bounds on
nontrivial cycle lengths, Discrete Mathematics, 118 (1993).
[Eli11] S. Eliahou, Le problème 3n+1 : y a-t-il des cycles non triviaux ? (III), sur le site Images des mathématiques (2011).
[Ger04]
D.-A. German, The golden mean shift is the set of 3x+ 1
itineraries, NKS conference (2004).
[Kra03]
I. Krasikov & J. Lagarias, Bounds
for the 3x+1 problem using difference inequalities, Acta Arith.,
109 (2003).
[Lag85] J. Lagarias: The 3x+1 problem and its generalizations, Amer. Math. Month., Volume 92 (1985).
[Lag-I] J. Lagarias, The 3x+1 problem annotated bibliography (1963-1999), arXiv (2011).
[Lag-II] J. Lagarias, The 3x+1 problem annotated bibliography, II (2000-2009), arXiv (2012).
[Lag11]
J. Lagarias, The Ultimate
Challenge: The 3x+1 Problem, American Mathematical Monthly (2010).
[Let99] S.
Letherman, D. Schleicher & R. Wood, The 3n+1 Problem and Holomorphic
Dynamics, Experimental Mathematics, Volume 8,
Issue 3 (1999).
[Lyg14] N. Lygeros & O. Rozier, Dynamique du problème 3x+1 sur la droite réelle, Ratio Matematica 26 (2014).
[Lyg19] N. Lygeros & O. Rozier, Paramétrisation du problème 3x+1 sur la droite réelle : diagramme de phase, renormalisation et intervalles errants, HAL (2019).
[Mat84] K. Matthews & A. Watts, A generalization of Hasse's generalization of the Syracuse algorithm, Acta Arith. 43 (1984).
[Pe04] J.L. Pe, The 3x+1 Fractal, Computers & Graphics, Volume 28, Issue 3 (2004).
[Poc17]
L.-O. Pochon & A. Favre, La suite de
Syracuse, un monde de conjectures, HAL (2017).
[Roz90] O. Rozier, Démonstration de l'absence de cycles d'une certaine forme pour le problème de Syracuse, Singularité N°3 (1990).
[Roz91] O. Rozier, Problème de Syracuse: "Majorations" élémentaires des cycles, Singularité Volume 2 N°5 (1991).
[Roz17] O. Rozier, The 3x+1 problem: a lower bound hypothesis, Funct. Approx. Comment. Math. 56 (2017).
[Roz19] O. Rozier, Parity sequences of the 3x+1 map on the 2-adic integers and Euclidean embedding, INTEGERS 19, A8 (2019).
[Sim17] R. Simonetto,
Conjecture de
Syracuse: avancées inédites, HAL (2017).
[Sin03] M. Sinisalo, On the minimal cycle lengths of the Collatz sequences (2003).
[Sté20] T. Stérin, The Collatz process embeds a base conversion algorithm, Reachability Problems conference (2020).
[Tao22] T. Tao, Almost all orbits of the Collatz map
attain almost bounded values, Forum of Mathematics, Pi 10
(2022).
[Ter76] R. Terras, A stopping time problem on the positive integers, Acta Arith. 35 (1976).
[Ter79] R. Terras, On the existence of a density, Acta Arith. 30 (1979).
[Ura02] T. Urata, Some holomorphic functions connected with the Collatz Problem, Bull. Aichi University of Education, 51 (2002).
[Wir98] G.J.
Wirsching, The Dynamical System
Generated by the 3n+1 Function, Springer-Verlag (1998).
Liens
Sites généralistes
Wikipedia
(français) : Conjecture
de SyracuseWikipedia (anglais) : Collatz conjecture
Mathworld : Collatz Problem
Sites de vulgarisation
Images des mathématiques : Le problème 3N+1 (I), (II), (III)Gérard Villemin : Cycle de Syracuse
Science étonnante : La conjecture de Syracuse
Quelques
vidéos instructives
(de la plus accessible à la plus ardue)
El Jj : La conjecture de Syracuse - Deux (deux ?) minutes pour... (15')Inigo Quilez : The Collatz Conjecture and Fractals (10')
Veritasium : The simplest math problem no one can solve (22')
Ivan Riou : Conway-maps, conjecture de Collatz et gamme musicale [Conference] (1h 05')
Math Kook : The Collatz Conjecture [62+ épisodes]
Terence Tao - The notorious Collatz conjecture [Conference] (50')
Marc Chamberland : The 3x+1 Problem: Status and recent work [Conference] (52')
Felipe Gonçalves : The Collatz Conjecture [Lectures] (~20h)
Vérification numérique de la conjecture
David Barina : Convergence verification of the Collatz problemTomás Oliveira e Silva : Computational verification of the 3x+1 conjecture
Eric Roosendaal : On the 3x + 1 problem
Recherches personnelles d'amateurs éclairés
Eric Farin : The Collatz Problem - Experimental Data and ModelsClaude Terracol : Conjecture de Syracuse
Fabien Toulgoat : Conjecture de Syracuse
Xander : The Collatz Fractal
Pages
de chercheurs
en mathématiques ou informatique
Marc
Chamberland : The
3x+1 Problem Jeffrey C. Lagarias : 3x+1 problem and related problems
Keith Matthews : 3x+1 page
Tristan Stérin : 6 Collatz tiles
Terrence Tao : What's new [blog]
Merci à J-P Delahaye pour ses encouragements, à Charles Vassallo pour ses précieux conseils, à Nik Lygeros et Claude Chaunier sans qui cette page n'aurait jamais vu le jour, à Matthew Cook, Jean-Jacques Daudin, Kevin Knight, Josefina López, Rénald Simonetto, Tristan Stérin et Claude Terracol pour les échanges fructueux que nous avons eus.
Olivier Rozier Ⓒ 2008

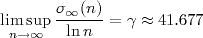
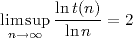


 +, continue
et linéaire par morceaux
+, continue
et linéaire par morceaux